MATH TEST (CALCULATOR)

55 MINUTES, 38 QUESTIONS

Questions 1 and 2 refer to the following information.

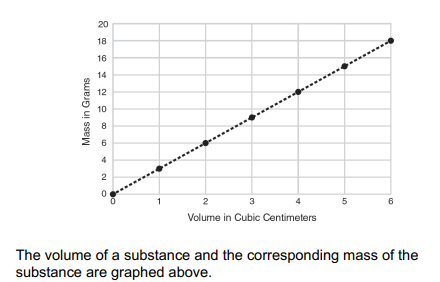
1. What equation represents the relationship between mass, m, and volume, v, in the above graph?

(A) ν = 3m

(B) m = 3ν

(C) m = 6ν

(D) ν = m + 2

2. Density equals mass divided by volume. What aspect of the function corresponds to the density of the substance?

(A) slope

(B) y-intercept

(C) x-intercept

(D) domain

3. What is the sum of the following polynomials?

(A) 30x⁶+ x³ − x + 1 

(B) 30x³ + 2x² + x − 1 

(C) 11x³ + x² − x + 1

 (D) 11x³ − x² + x − 1

4. What is the median of this set of numbers?

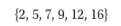
(A) 7

(B) 8

(C) 8.5

(D) 9

5. Between which years did enrollment stay steady?

(A) 1990–1991

(B) 1992–1993

(C) 1993–1994

(D) 1996–1997

 

Questions 6 and 7 refer to the following information.

The equation for gravitational force, F_g, is the following:

G is the gravitational constant, m₁ and m₂ are the masses of objects, and r is the distance between the objects.

6.   How would the gravitational force between two objects change if the distance between the objects doubles while all other quantities remain the same?

(A) It would be twice the original force.

(B) It would be four times the original force.

(C) It would be 1/2 of the original force.

(D) It would be 1/4 of the original force.

7. What is the value of m₂ in terms of the other values in the equation?

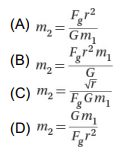
8. If the graph of the above function is written in the form  ax + by =3, in which a and b are constants, what is the sum of a and b?

(A) − 3

(B) − 1

(C) 2

(D) 5

9. There are 3 teaspoons in a tablespoon and 16 tablespoons in a cup. How much of a cup would there be in 12 teaspoons?

(A) 1/12 cup

(B) 1/4 cup

(C) 2 cups

(D) 6 cups

10. If a + 2b = 11 and 3a − 2b = 1, what is the value of a?

(A) − 3

(B) 1

(C) 2

(D) 3

11. Which of the following is an equivalent form of z = x − y?

(A)

(B)

(C)

(D)

12. Suppose the price of a product is typically p dollars. If a 30% discount is applied to the price, what is the discounted price in terms of p?

(A) 0.03p

(B) 0.3p

(C) 0.7p

(D) 1.3p

13. Tran runs a 5 km (5,000 m) race. Given that there are 0.3048 meters in 1 foot, approximately how many feet did he run in the race?

(A) 0.174

(B) 1,524

(C) 2,088

(D) 16,400

14.  If a point on the above line has an x value of a, what is the value of the point’s y-coordinate in terms of a?

(A) -1/3a

(B) -1/2a

(C) -3a

(D) 3a

Pet Owners Who Have Only One Pet

15.   If there were a randomly selected pet owner from the table above, what is the probability that it would be a male cat owner?

(A) 40/188

(B) 40/100

(C) 60/188

(D) 40/78

16. Due to radiation, the mass of a substance decreases by 0.5% of that day’s mass every day. Which type of function would properly model the mass of the substance as the days go by?

(A) Increasing linear

(B) Decreasing linear

(C) Increasing exponential

(D) Decreasing exponential

17. Jane is watering her garden and spends 5 minutes watering each tree and 2 minutes watering each shrub. If she can spend no more than 30 minutes watering her garden, which inequality represents the number of T trees and S shrubs she can water given these constraints?

(A) 5T + 2S ≥ 30

(B) 5T + 2S ≤ 30

(C) 5 × T × S ≤ 30

(D) 5 > 30 × T × S

Questions 18–19 refer to the following information.

Travel Statistics on Journey from Times Square to Harlem in New York City 

 

18. If Sarah took the subway from Times Square to Harlem, what was her speed in miles per hour, to the nearest tenth?

(A) 0.7 MPH

(B) 3.4 MPH

(C) 17.6 MPH

(D) 204.0 MPH

19. If Johann rode his bicycle to Harlem and then took a car back to Times Square (using the times and distances estimated in the table above), what was his speed in miles per hour for the entire time he travelled, to the nearest tenth?

(A) 9.2 MPH

(B) 12.2 MPH

(C) 14.6 MPH

(D) 551.2 MPH

20. A particular line is graphed in the xy-plane and uses only real numbers. The line has a positive slope and a positive y-intercept. Which of these points could be on the line?

(A) (−4, 5)

(B) (2, 0)

(C) (3, −6)

(D) (0, −1)

21. What percentage of 70 is 35?

(A) 40%

(B) 50%

(C) 75%

(D) 200%

22. Kamini wants to make money from recycling aluminum cans and glass bottles. Her local government pays her $0.10 per can and $0.16 for each bottle. If she wants to earn a total of at least $100 and has collected a total of 600 cans (and cannot collect any more cans), what is the minimum number of bottles she would need to collect to reach her goal?

(A) 250

(B) 270

(C) 300

(D) 420

Questions 23 and 24 refer to the following material.

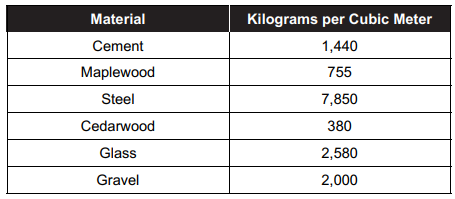
The density of different building materials is presented in the table above.

23. Based on the information in the table above, what is the weight of a solid steel wall that has a volume of 300 cubic meters?

(A) 26 kilograms

(B) 8,150 kilograms

(C) 432,000 kilograms

(D) 2,355,000 kilograms

24. The weight of a 20 cubic meter block of cement is what percent(to the nearest whole number) greater than the weight of a block of cedarwood of the same volume?

(A) 82%

(B) 279%

(C) 288%

(D) 1,282%

25. Students at a university were surveyed as to whether they wanted a new library for the university. Out of the 100 students surveyed, 40% said they wanted a new library. What is justifiable based on this information?

(A) Of the 100 students surveyed, 40 wanted a new library.

(B) Of all people in the university community, 40% want a new library.

(C) Exactly 40 students at the university want a new library.

(D) No more than 40 university students want a new library.

26. The function f is expressed as f(x) = k for all values of x, and k is a constant real number. Which of the following must be true?

I. f(x) forms a line.

II. f(x) has a slope of zero.

III. f(x) has a range from − ∞ to + ∞.

(A) I only

(B) II only

(C) Only I and II

(D) Only II and III

27. There are 10 cards, each distinctly numbered from 1 to 10. After a card is selected from the set, it is returned to the set. If someone first picks a 3 and then picks a 2, what is the probability that on the third selection the person will pick a 9?

(A) 1/20

(B) 1/10

(C) 1/9

(D) 1/6

28. In a right rectangular prism, the smallest edge is 2 cm long. The next greatest edge is twice the length of the smallest edge, and the greatest edge is 3 times the length of the smallest edge. What is the surface area of the prism?

(A) 6 sq cm

(B) 24 sq cm

(C) 64 sq cm

(D) 88 sq cm

29. If square ABCD has an area of 36 square units, what is the perimeter of square WXYZ, given that each vertex of square WXYZ bisects the side of square ABCD that it intersects?

(A) 6

(B)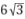 

(C) 12

(D)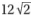

30. The price of a video streaming service increases by 15% each year. If the price, P, of the service begins at v dollars, what is the value of the constant c in the following function that models the price of the service t years after it begins?

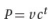
(A) 0.15

(B) 0.85

(C) 1.15

(D) 1.55

31. If , what is the value of x?

32. Triangle ABC has a right angle B. If side AB has a length of 7 units and side BC has a length of 24 units, what is the length in units of side AC?

33. The total calories for a particular salad are 1,100. The salad consists of only cheese, vegetables, and dressing. If the total caloric value of the cheese and vegetables is 650, and each packet of dressing used on the salad has 75 calories, how many packets of dressing were used on the salad?

34. The solution to the above system of equations is (a, b). What is the value of a − b?

35. In the above equation, a is a constant. The equation has infinitely many solutions. What is the value of a?

36. Water from the ocean has 3.5% salt, and water from the Dead Sea has 33.7% salt. If someone has 10 gallons of ocean water, how many gallons of water from the Dead Sea (measured to the nearest hundredth of a gallon) need to be added so that the solution has 10% salt?

37. The mean height of 7 teenage boys is 67 inches. If one of the boys has a height of 74 inches, what is the mean height of the remaining boys to the nearest tenth of an inch?

38. The function above portrays the height, h, of a projectile t seconds after being thrown. Which of the following would be the time in seconds at which the height of the projectile is at its maximum value?